| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 자바
- level3
- LEVEL2
- Github
- 휴학
- androidstudio
- Python
- 컨트리뷰톤
- BFS
- 컴퓨터비전
- SQL
- 다시풀기
- 파이썬
- git
- java
- build
- 프로그래머스
- SWEA
- Matrix Factorization
- WebOS
- level4
- 내휴학생활중의아주큰일
- MSBuild
- 대학원
- 어렵다
- level1
- 대학원일기
- D3
- 안드로이드스튜디오
- py
Archives
- Today
- Total
bit가 눈 앞에서 왔다갔다
py) BFS, DFS 본문
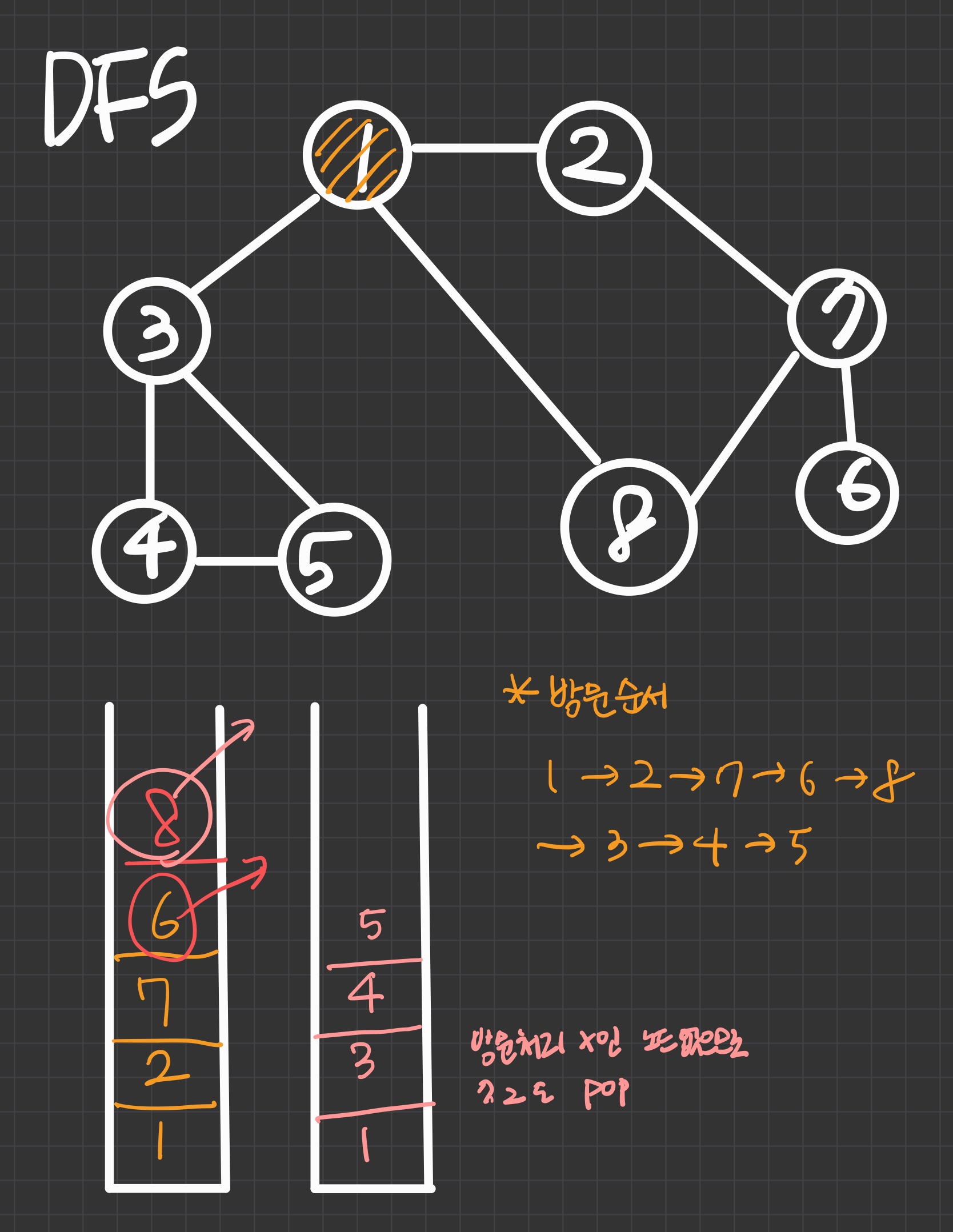
DFS(Depth First Search) 깊이 우선 탐색
: 시작 노드를 방문처리 하고 방문처리 되지 않은 노드로 진행 선택된 노드는 방문처리 되고 새로운 시작 노드가 되어 같은 방법을 반복하다가 방문처리 되지 않은 노드가 없을 경우 되돌아 감
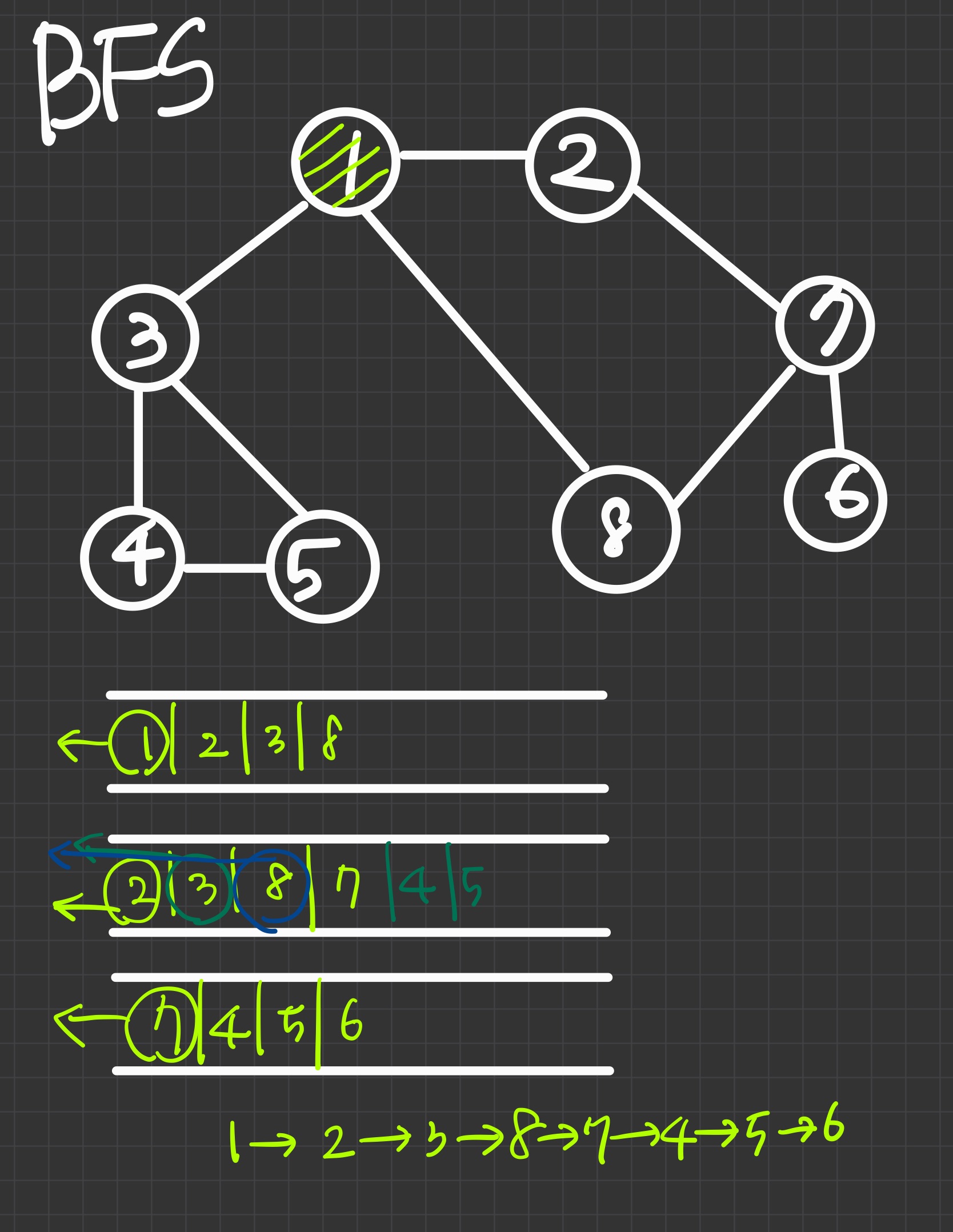
BFS(Breadth First Search) 너비 우선 탐색
: 시작 노드로부터 가까운 노드를 먼저 방문하고 멀리 떨어져 있는 노드를 나중에 방문. 시작 노드에서 인접한 노드들을 방문하고 그 노드들과 인접한 노드들을 방문
DFS
-구현 가능한 방법 또는 활용하는 자료구조: 1. 순환호출(재귀함수) 2. 스택(Stack)
- 순환호출 이용
def dfs(graph, v, visited):
visited[v] =True
print(v, end=' ')
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited) #재귀
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5], #3
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [False] * 9 #방문을 체크하기 위한 빈 리스트 (방문안됨 처리)
dfs(graph, 1, visited)
#1번 노드부터 방문 시작
BFS
-사용하는 자료구조: 큐(Queue)
from collections import deque #deque 사용
def bfs(graph, start, visited):
queue = deque([start]) #queue 사용
visited[start] = True
while queue:
v = queue.popleft()
print(v, end=' ')
for i in graph[v]:
if not visited[i]:
queue.append(i)
visited[i] = True
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5], #3
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [False] * 9 #방문을 체크하기 위한 빈 리스트 (방문안됨 처리)
bfs(graph, 1, visited)
#1번 노드부터 방문 시작
느낀점: 이 코드만 외운다거나 꽂히거나 할 게 아니라 개념을 이해해서 문제에 따라 잘 활용하는게 필요!
참고 - youtu.be/7C9RgOcvkvo
반응형
'Algorithm > Concept' 카테고리의 다른 글
| Py) 퀵정렬 Quick Sort (0) | 2021.02.17 |
|---|---|
| Py) 삽입정렬 Insertion Sort (0) | 2021.02.17 |
| Py) 선택정렬 Selection Sort (0) | 2021.02.17 |
| Union-Find(Disjoint-Set) 합집합 찾기 (0) | 2019.11.19 |
| BFS(Breadth First Search) 너비우선탐색 (5) | 2019.11.04 |
Comments

