| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- WebOS
- 안드로이드스튜디오
- level1
- 대학원
- 컨트리뷰톤
- Matrix Factorization
- SQL
- java
- 파이썬
- SWEA
- level4
- 프로그래머스
- 어렵다
- git
- build
- py
- 내휴학생활중의아주큰일
- 자바
- MSBuild
- level3
- 대학원일기
- D3
- Python
- androidstudio
- LEVEL2
- Github
- 컴퓨터비전
- BFS
- 다시풀기
- 휴학
- Today
- Total
bit가 눈 앞에서 왔다갔다
Py) 프로그래머스 62048 멀쩡한 사각형 본문
https://programmers.co.kr/learn/courses/30/lessons/62048
코딩테스트 연습 - 멀쩡한 사각형
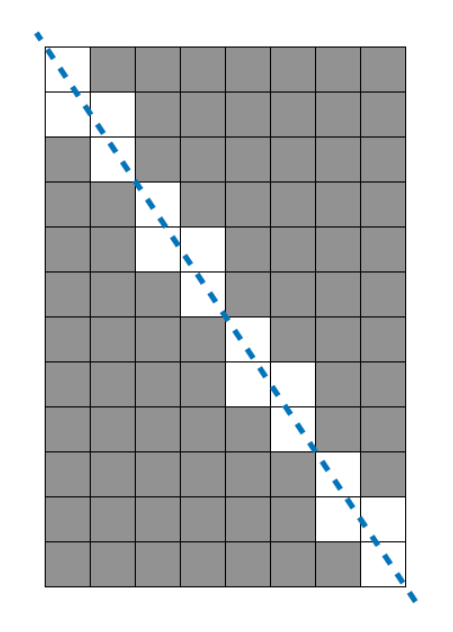
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을
programmers.co.kr
1차시도: 45분
2차시도: 15분
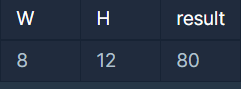
1. 입출력
2. 내 접근
1) 이건 그냥 지나가는 개수 찾는 공식?만 생각하면 쉽게 풀리겠다.
2) 피타고라스 정리를 떠올림
2-1) 사각형 몇 개 그려보며 이런 저런 생각을 시작함.
w == h면 w 또는 h 크기만큼 못쓴다는건 너무 당연
최소공약수가 존재할 경우, 비율에 따라 최소로 w,h를 줄이고 제곱해서 루트한 수에 floor 함수 적용
존재하지 않을 경우, 제곱해서 루트한 수의 정수값에 +1을 해주자
-> 머신러닝에서는 이런 식으로 트레이닝 데이터에 딱 맞게 모델을 설계하면 과적합 문제가 발생해, 새로운 데이터에서 잘못 작동해버린다.
2-2) 위와 같이 하다가 5:4에서는 또 그게 아님을 찾았고, 잘못하고 있다는 생각에 솔루션을 찾아보기로 함
접근이 유사하긴했음... 그냥 더 해볼껄 그랬나))
3. Solution
3-1. 알고리즘
1) 두 수가 서로소가 아니라면
1-1) 두 수를 최대공약수로 나눈 수로 두 수를 나눈다.
1-2) 그때 w와 h 중 가장 큰 값만큼 잘리게 되어있음
1-3) 최대공약수 만큼 반복된다.
2) 서로소라면, w+h-1임
3-2. 코드
def solution(w,h):
answer = 1
gcd = 1
small = w if w < h else h
for i in range(1, small+1):
if w % i == 0 and h % i == 0:
gcd = i # 최대공약수를 찾는다
answer = w*h - (w//gcd + h//gcd-1)*gcd
return answer
4. 피드백
w/i ==0 or h/i ==0 이라고 했는데 1. 몫은 0이 나올 수가 없음, 2. or로 하면 최대공약수 아님
w+h-1 을 생각해내는게 포인트 였던 것 같다.
5. 새롭게 알게 된 것들
* math.gcd
위의 코드로 짜면 시간이 엄청 오래 걸리는 게 나온다

import math
def solution(w,h):
answer = 1
return answer = w*h - (w+h - math.gcd(w,h))이렇게 gcd 함수를 사용하면 전부 0.00대로 통과가 가능하고
* 유클리드 호제법을 이용하는 방법도 있다.
유클리드 호제법 참고 - https://velog.io/@yerin4847/W1-%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C-%ED%98%B8%EC%A0%9C%EB%B2%95
간단하게 말해서 mod 연산을 반복하고, 나머지가 0이 될때 mod 연산에 사용한 몫이 두 수의 최대공약수이다.
'Algorithm > Prob' 카테고리의 다른 글
| Py) 프로그래머스 67258 보석 쇼핑 (0) | 2022.03.25 |
|---|---|
| Py) 프로그래머스 64061 크레인 인형뽑기 게임 (0) | 2022.03.23 |
| Py) 프로그래머스 17676 [1차] 추석 트래픽 (0) | 2022.03.16 |
| Py) 프로그래머스 64063 호텔 방 배정 (0) | 2022.03.11 |
| Py) 프로그래머스 67259 경주로 건설 (0) | 2022.03.10 |




